Scalable Penalized Regression

摘要

SPR是一个有理论保证的干净样本选择算法，用于含噪学习中。 本文针对含噪学习中的样本选择问题，首先介绍我们发表在CVPR22的算法SPR，该算法在不可表示（irrepresentable）条件下所识别的噪声样本为真实噪声样本的子集，进一步的，在大误差（large error）条件下能够保证所识别的噪声样本集等于真实噪声样本集。在实际应用中，我们无法知晓不可表示条件是否得到满足，在这种情况下，我们提出在一般性的干净样本选择算法中，控制干净样本的错误选择率（False-Selection-Rate, FSR）是至关重要的。基于此，我们提出Knockoffs-SPR，该算法能够将FSR控制在预先指定的上界\(q\)之下。

背景

在分类问题中，神经网络往往需要大量的有标签数据进行训练。在这个过程中，标签的正确性至关重要。由于神经网络具有强大的拟合能力，对随机生成的标签也能有效拟合，因此用于训练的数据标签出现错误时，会对神经网络的分类能力造成破坏。本文研究在含有错误标签的训练集中选择无错误标签子集的样本选择算法，去除数据集中的标签噪声，使神经网络能够更好的进行训练。在本文中，我们称标签错误的样本为噪声样本，标签正确的样本为干净样本。

框架

Knockoffs-SPR 在网络学习和样本选择之间运行一个循环。我们基于特征和one-hot向量之间的近似线性关系刻画标签的可信度，从中选择干净样本。

在SPR中，我们对神经网络特征和one-hot标签之间的关系进行线性近似。该线性近似是很弱的，因此如果一个很弱的近似依然能够很好的拟合一个样本的特征标签对，我们就认为该样本是干净样本；而如果该近似不能很好的拟合一个样本，该样本就很可能是噪声样本。基于这种差异性，我们引入变量刻画线性模型对样本的拟合程度，通过对该变量的求解得出每个样本的可信度，从而筛选出干净样本。

依据LASSO的模型选择理论，我们可以证明在一定条件下，SPR能够识别出所有噪声样本。

然而，SPR的理论条件在现实中无法提前知道是否成立，因此现实意义有限。当SPR的理论条件不成立时，所选择的干净样本中可能存在噪声样本。为了解决这个问题，我们的期刊拓展文章中提出了Knockoffs-SPR。

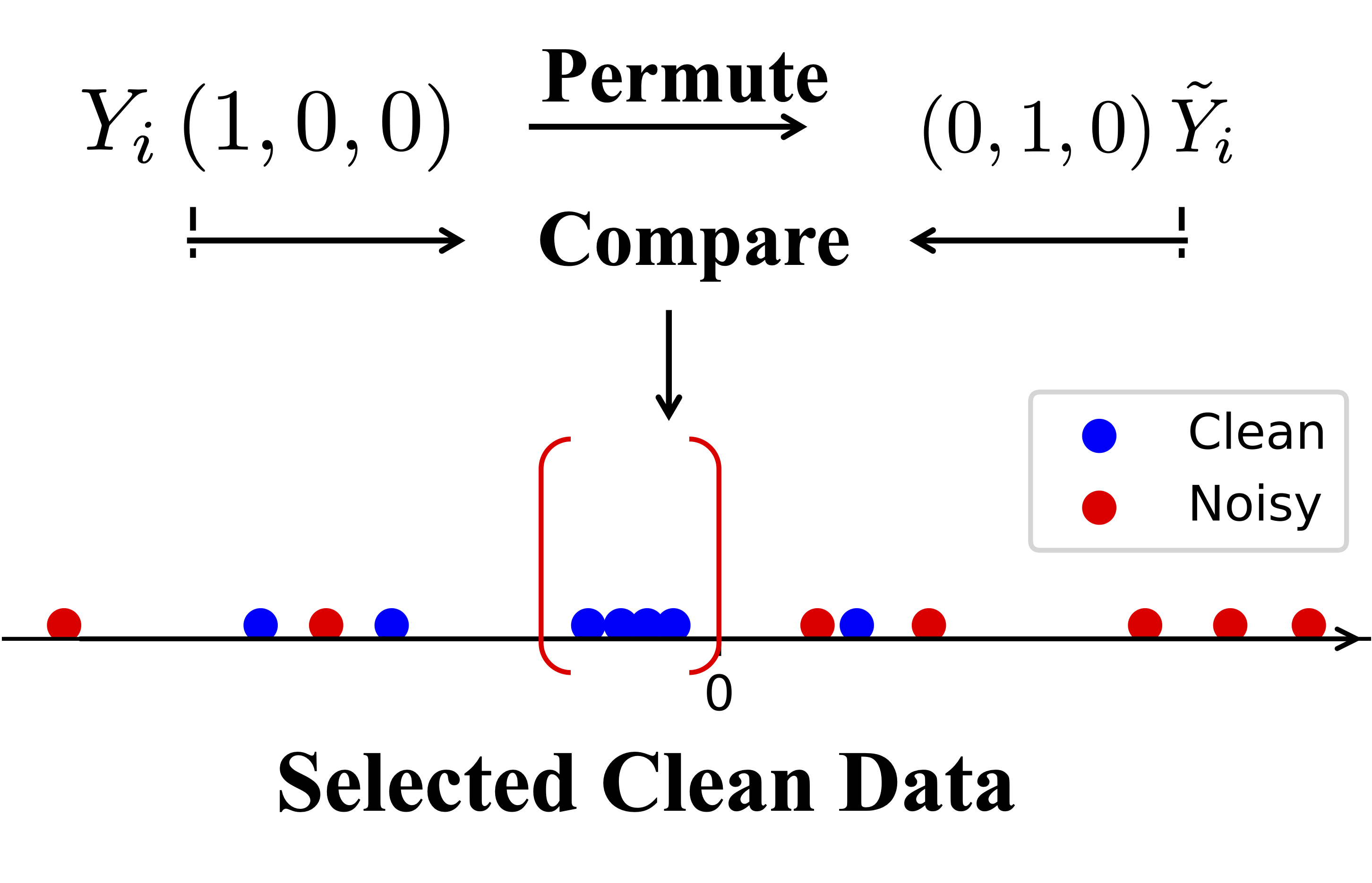
在Knockoffs-SPR中，我们研究在一般的样本选择环境中，尽可能的控制干净样本的错误选择率。我们同样依赖于神经网络特征和one-hot标签之间的关系的线性近似。但是在Knockoffs-SPR中，我们首先关注于单个样本，将其标签的可信度与一个随机置换（permute）的标签的可信度进行比较。这两者的对比在该样本的标签为干净标签和噪声标签时具有不同的表现，我们基于这种差异性构建比较统计量。之后，我们对每个样本的比较统计量在样本之间进行比较，筛选出可信的样本。我们证明，在这样的一系列构造下，Knockoffs-SPR天然的能够控制干净样本的错误选择率。

接下来我们对SPR和Knockoffs-SPR的算法细节和理论结果进行介绍。

SPR

我们从神经网络中隐含的线性关系开始。 对于经过理想训练的网络，我们在特征向量和one-hot标签之间有： \[y_i=\textrm{SoftMax}(x_i^{\top}\beta)\] 我们通过删除 soft-max 运算符来近似该关系： \[y_i=x_i^{\top}\beta+\varepsilon_i\] 这个近似很弱，但对我们的目标很有帮助。

众所周知，线性回归模型对异常值非常敏感。 我们可以使用预测误差来识别它们 \[r_i=y_i-x_i^{\top}\hat{\beta}\] 或者更统计地，使用留一法检验假设。 但当我们有大量训练数据时，对每个样本单独进行留一法检验假设的成本是无法接受的。 因此，我们引入一个显式参数 \(\gamma_i\)来表示预测误差。我们有 \[y_i=x_i^{\top}\beta+\gamma_i+\varepsilon_i\] 对于干净的数据，特征和标签之间的线性关系很强，因此我们应该有一个小的甚至为零的 \(\Vert\gamma_i\Vert\)。 如果数据被错误标记，线性模型很难拟合该数据，将返回一个大的 \(\Vert\gamma_i\Vert\)。 基于干净样本与噪声样本的这种差异，我们设计算法利用\(\gamma_i\)将两者区分开。

现在我们的目标是求解此模型中的 \(\gamma_i\) ，其中\(\gamma_i = 0\)对应的样本为干净样本， \(\gamma_i\neq 0\) 对应的样本为噪声样本。 我们的优化问题如下： \[(\hat{\beta},\hat{\gamma})=\underset{\beta,\gamma}{\mathrm{argmin}}\Vert Y-X\beta-\gamma\Vert_\mathrm{F}^2+\lambda R(\gamma)\] 通过找到 \(\beta\) 关于 \(\gamma\) 的闭式解，经过一些变量替换，我们可以将问题转化为 \[\underset{\gamma}{\mathrm{argmin}}\left\Vert \tilde{Y}-\tilde{X}\gamma\right\Vert_\mathrm{F}^2+\lambda R\left(\gamma\right)\]

由于很难提前选择合适的 \(\lambda\)，我们改为将估计值 \(\hat{\gamma}\) 视为 \(\lambda\) 的函数。 然后我们可以生成 \(\hat{\gamma}\) 关于 \(\lambda\) 的解路径：

我们使用使 \(\hat{\gamma}_i\) 变为零的 \(\lambda\) 的值对数据进行排序，如下所示： \[C_{i}=\sup \left\{\lambda: \gamma_{i}(\lambda) \neq 0\right\}\] 其中，最后消失的样本为噪声样本（图示红色线条），最先消失的样本为干净样本（图示蓝色线条）。在实际使用中，我们选择50%的样本为干净样本。

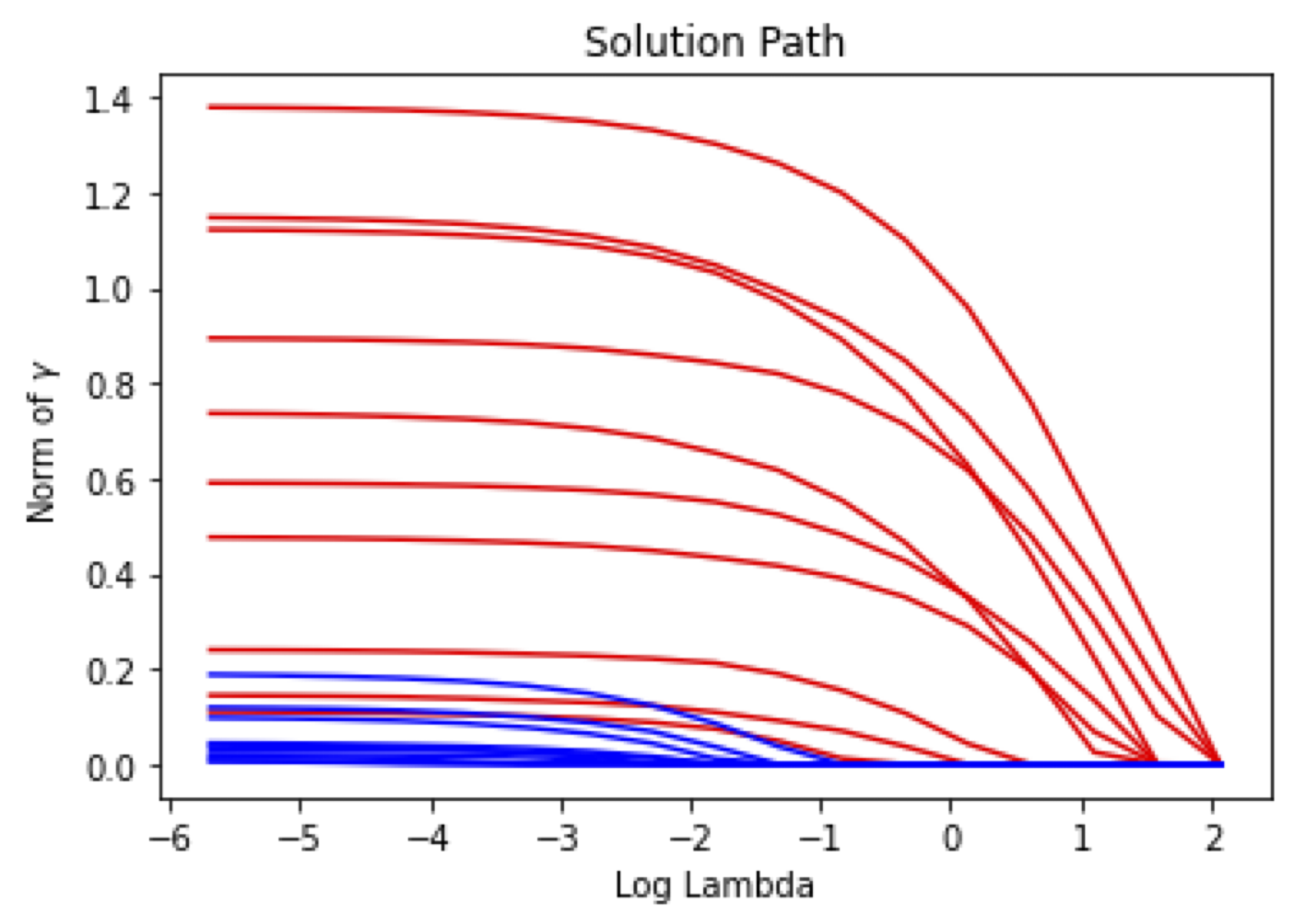
SPR的噪声集恢复理论

基于LASSO模型的模型选择理论，我们可以为具有L1惩罚的SPR的噪声集恢复提供理论。 假设 \(\varepsilon\) 是零均值亚高斯噪声。 我们给出三个条件：

• (C1: 特征值约束) \[\lambda_{\min}(\mathring{X}_{S}^{\top}\mathring{X}_{S})=C_{\min} >0\]
• (C2: 不可表示性) \(\exists\ \eta\in\left(0,1\right]\), \[\Vert\mathring{X}_{S^c}^{\top}\mathring{X}_{S}(\mathring{X}_{S}^{\top}\mathring{X}_{S})^{-1}\Vert_\infty \leq 1-\eta \]
• (C3: 大误差) \[\gamma^*_{\min}:= \min_{i\in S}|\gamma^*_{i}|>h(\lambda,\eta,\mathring{X},\gamma^*)\] 其中 \(\Vert A\Vert_\infty:= \max_i \sum_j |A_{i,j}|\), \(h(\lambda,\eta,\mathring{X},\gamma^*)=\lambda\eta/\sqrt{C_{\min}\mu_{\mathring{X}}}+\lambda \Vert(\mathring{X}_{S}^{\top}\mathring{X}_{S})^{-1}\mathrm{sign}(\gamma_{S}^*)\Vert_\infty\)。

基于这些条件，我们可以给出以下定理：

定理(SPR的噪声集恢复理论)。 令 \(\lambda\geq \frac{2\sigma \sqrt{\mu_{\mathring{X}}}}{\eta}\sqrt{\log cn}\)。 那么在概率大于\(1-2(cn)^{-1}\)的情况下, SPR有唯一解\(\hat{\gamma}\)使得:

• 如果 C1 和 C2 成立，SPR识别的噪声集是真实噪声集的子集；
• 如果 C1、C2 和 C3 成立，SPR 可以识别所有噪声数据。

基本上，这个定理告诉我们，如果我们有 C1，我们可以获得唯一解。 如果 C2 成立，干净的数据和嘈杂的数据在某种程度上是不同的，这能够让SPR识别出一部分噪声数据。 如果我们有 C3，则误差大到足以从随机噪声中识别出来，那么SPR将能够识别所有噪声数据。

Knockoffs-SPR

噪声集恢复定理中的不可表示条件和真实噪声集的信息实际上是未知的，使得该理论很难在现实生活中使用。 特别是，在真实噪声集未知的情况下，算法可能会在不适当的时间停止，从而导致所选干净数据的噪声率仍然很高，使下一轮训练的模型被噪声严重破坏。

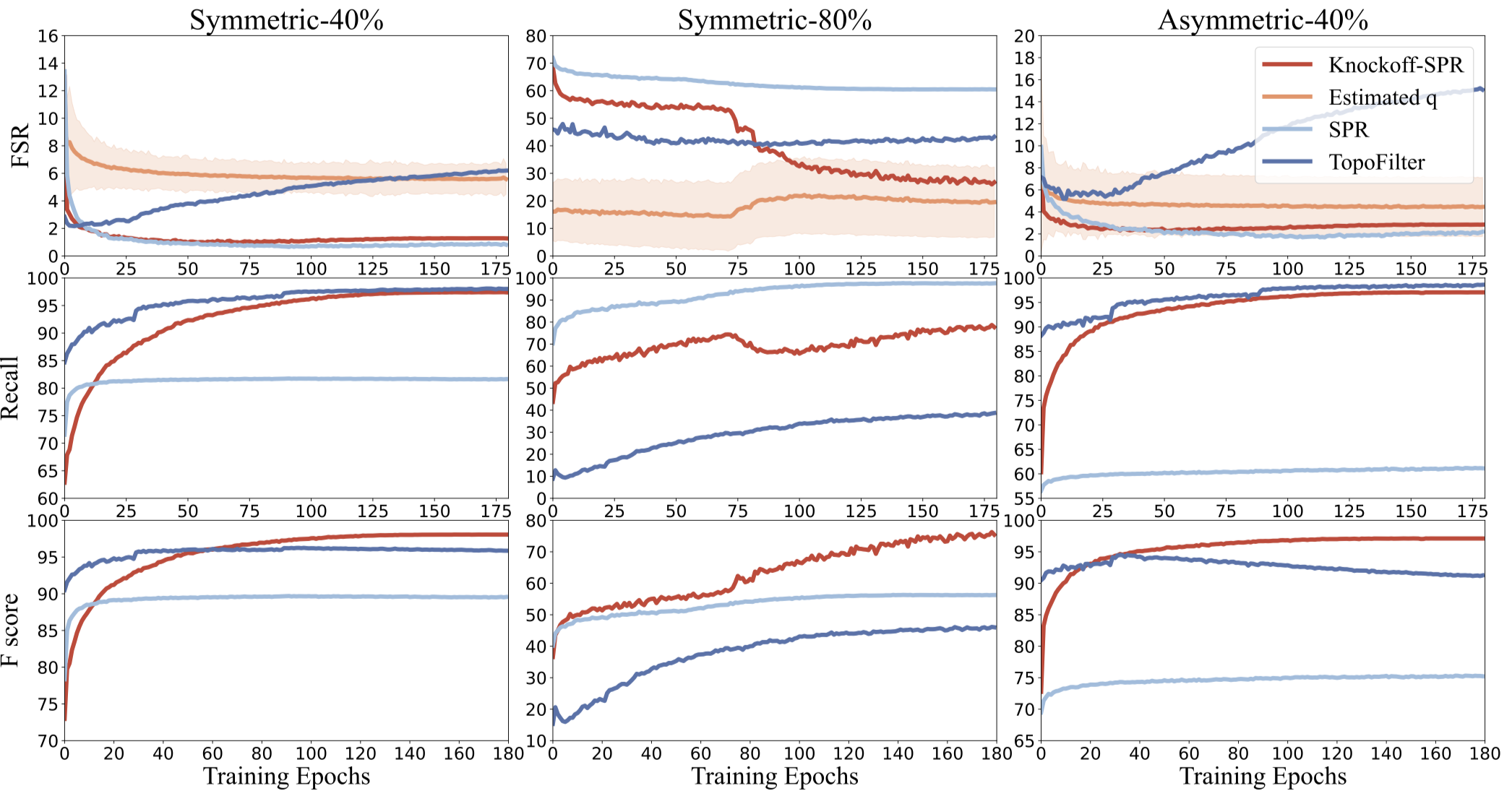
为了解决 SPR 中的错误选择问题，我们在本节中提出了一种数据自适应的样本选择方法，其目标是控制所选数据的预期噪声率，称为错误选择率（False-Selection-Rate, FSR），在期望水平 \(q\) (\(0 < q < 1\)): \[ \mathrm{FSR}=\mathbb{E}\left[\frac{\#\left\{ j: j\not\in \mathcal{H}_0 \cap \hat{C}\right\} }{\#\left\{ j:j\in\hat{C}\right\} \lor1}\right], \] 其中 \(\hat{C}=\{j:\hat{\gamma}_j= 0\}\) 是我们所估计的干净集，\(\mathcal{H}_0: \gamma^*_i = 0\) 表示零假设，即样本 \(i\)属于干净数据集。 因此，FSR 的目标是控制选定原假设中的错误率，也称为假设检验中 II 类错误的期望。

具体而言，我们将整个数据 \(\mathcal{D}\) 拆分为 \(\mathcal{D}_1:=(X_1,Y_1)\) 和 \(\mathcal{D}_2:=(X_2,Y_2 )\)，并在 \(\mathcal{D}_1\) 和 \(\mathcal{D}_2\) 上分别运行 Knockoffs-SPR。 下面我们只介绍Knockoffs-SPR在\(\mathcal{D}_2\)上选择干净样本的过程，在\(\mathcal{D}_1\)的选择过程是类似的。 粗略地说，该过程由三个步骤组成： i) 在\(\mathcal{D}_1\)上估计 \(\beta\); ii) 在 \(\mathcal{D}_2\) 上估计 \(\tilde{\gamma}(\lambda))\); 和iii)构建比较统计量和选择过滤器。

步骤 i): 在 \(\mathcal{D}_1\) 上估计 \(\beta\)。 我们的目标是提供独立于 \(\mathcal{D}_2\) 的 \(\beta\) 的估计值。 最简单的策略是使用标准 OLS 来获得 \(\hat{\beta}_1\)。 然而，这个估计值可能不准确，因为它被噪声样本破坏了。 出于这个考虑，我们首先在 \(\mathcal{D}_1\) 上运行 SPR 以获得干净的数据，然后通过 OLS 使用SPR估计的干净数据求解 \(\beta\)。

步骤 ii): 在\(\mathcal{D}_2\)上估计 \(\left(\gamma(\lambda),\tilde{\gamma}(\lambda)\right)\). 在\(\mathcal{D}_1\)得到估计值\(\hat{\beta}_1\)后，我们在\(\mathcal{D}_2\)上估计 \(\gamma(\lambda)\)： \begin{equation} \frac{1}{2}\left\Vert Y_2-X_2\hat{\beta}_1-\gamma_{2}\right\Vert_{\mathrm{F}}^{2}+P(\gamma_{2};\lambda). \end{equation} 对于每个 one-hot 向量 \(y_{2,j}\)，我们随机置换 1 的位置并获得另一个 one-hot 向量 \(\tilde{y}_{2,j}\neq y_{2 ,j}\)。 对于干净的数据 \(j\)，\(\tilde{y}_{2,j}\) 变成了一个错误标签； 而对于噪声数据，\(\tilde{y}_{2,j}\) 以 \(\frac{c-2}{c-1}\) 的概率变为另一个噪声标签，以 \(\frac{1}{c-1}\)的概率变为一个干净标签。 在获得置换矩阵 \(\tilde{Y}_2\) 后，我们使用与 SPR 相同的算法求解路径 \(\left(\gamma_{2}(\lambda), \tilde{\gamma}_2(\lambda)\right )\) ： \begin{equation} \begin{cases} \frac{1}{2}\left\Vert Y_2-X_2\tilde{\beta}_1-\gamma_2\right\Vert _{\mathrm{F}}^{2}+\sum_j P(\gamma_{2,j};\lambda),\\ \frac{1}{2}\left\Vert \tilde{Y}_2-X_2\tilde{\beta}_1-\tilde{\gamma}_2\right\Vert _{\mathrm{F}}^{2}+\sum_j P(\tilde{\gamma}_{2,j};\lambda). \end{cases} \end{equation}

步骤 iii): 比较统计量和选择过滤器。 在获得解路径 \(\left(\gamma_{2}(\lambda), \tilde{\gamma}_2(\lambda)\right)\) 后，我们定义关于 \(Y_{2 ,i}\) 和 \(\tilde{Y}_{2,i}\) 中每个样本 \(i\) 的选择时间： \(Z_i := \sup\{\lambda: \Vert \gamma_{2,i}(\lambda) \Vert_2 \neq 0\}\) 和 \(\tilde{Z}_i := \sup\{\lambda: \Vert \tilde{\gamma}_{2,i } (\lambda) \Vert_2 \neq 0\}\)。 我们的出发点为，对于干净样本，我们将更可能有\(Z_i < \tilde{Z}_i\)，而对于噪声样本，若其置换标签依然为噪声标签，我们无法判断\(Z_i, \tilde{Z}_i\)的大小关系，因此假设\(Z_i < \tilde{Z}_i\)与\(Z_i > \tilde{Z}_i\)的概率接近，而若置换标签为干净标签，则更可能有\(Z_i > \tilde{Z}_i\)。基于这种差异性，使用\(Z_i, \tilde{Z}_i\)，我们构造比较统计量为 \begin{equation} \label{eq:w} W_i := Z_i \cdot \mathrm{sign}(Z_i - \tilde{Z}_i). \end{equation} 根据该比较统计量，我们定义一个数据自适应的选择阈值\(T\) \begin{equation} T=\max\left\{ t>0:\frac{1 + \#\left\{ j:0 < W_{j} \leq t\right\} }{\#\left\{ j:-t\leq W_{j} < 0 \right\} \lor 1}\leq q\right\}, \end{equation} 或者 \(T=0\) 如果这个集合是空集。 其中 \(q\) 是预先定义的上界。 我们的算法通过\(T\)选择干净样本如下： \begin{equation} \label{eq:clean-set} C_2:=\{j:-T\leq W_j < 0 \}. \end{equation} 根据经验，如果阈值 \(q\) 足够小，\(T\) 可能等于 \(0\)。 这时，我们的算法没有选择任何干净数据，这是没有意义的。 因此，我们从一个小的 \(q\) 开始并迭代地增加 \(q\) 并计算 \(T\)，直到可获得的 \(T\) 使得 \(T > 0\) 且FSR 约束的尽可能小。 当 FSR 不能被 \(q=50\%\) 限制时，我们将结束选择并通过 \(\{W_j\}\) 简单地选择一半最可能的干净样本。

Knockoffs-SPR的FSR控制理论

我们的目标是用我们的数据自适应阈值 \(T\) 来证明在我们所选择的干净样本中 \(\mathrm{FSR}\leq q\)。 我们的主要结果如下：

定理(FSR控制理论). 对\(c\)类别的分类任务, 对于任意 \(0 < q \leq1\), Knockoffs-SPR的解满足 \begin{equation} \mathrm{FSR}(T)\leq q \end{equation} 其中\(T\)对两个子集分别定义为 \begin{equation*} T_i=\max\left\{ t\in\mathcal{W}:\frac{1+\#\left\{ j:0 < W_{j}\leq t\right\} }{\#\left\{ j:-t\leq W_{j} < 0 \right\} \lor 1}\leq \frac{c-2}{2c}q\right\}. \end{equation*}

这个定理告诉我们，FSR 可以使用 Knockoffs-SPR 的算法由给定的阈值 \(q\) 控制。 与 SPR 相比，此算法在实际实验中更实用和有用。

实验

我们对两个合成标签噪声数据集 CIFAR-10 和 CIFAR-100 进行了实验。 我们还在两个真实世界的嘈杂数据集 WebVision 和 Clothing1M 上测试了 Knockoffs-SPR。实验结果如下：

同时，我们以CIFAR-10为例，在不同的噪声环境中测试了几个样本选择算法选择干净样本的质量，结果如下： 可以看出，Knockoff-SPR能够很好的控制FSR，同时在整体样本选择质量（F-score）上占据优势。 更多细节请阅读我们的论文 (CVPR22,TPAMI23)。